Panoráma bővített kockaráccsal

Kivételes esetekben felmerülhet látómezőnk tágításának igénye.

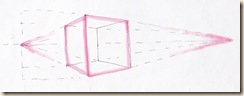
Vajon egyenesek maradnak-e a befoglaló kockaháló rúdjai panoráma esetében?

Képkivágás-kereső vázlat színes krétával.

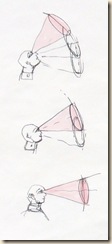
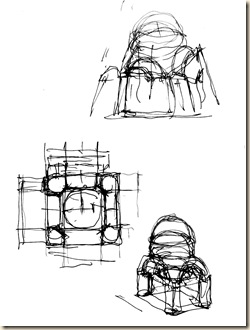
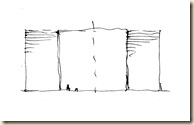
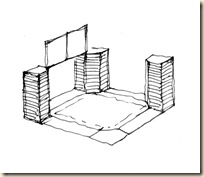
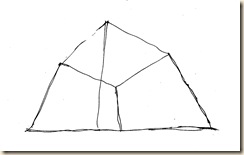
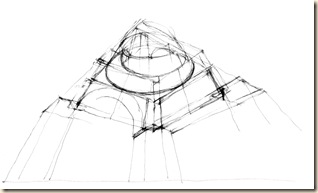
Első eset: a budapesti Bazilika impozáns kupolaterének látványát oszlop-lábazattól kupola-koronáig egyetlen rajzlapba sűrítjük. Legalább három szokványos látókúpot használunk.

Először egyenesen előre, majd feljebb tekintünk.

Nyakunkat vízszintes tengely körül billentve, tekintetünket megemeljük.

Ilyen módon látómezőnket az egyik főtengely mentén kiterjesztjük. Sávos panorámát kapunk. Foltokból összerótt képsíkunk nyolcad-gömb szeletre hasonlít.

 

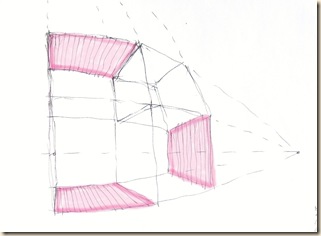
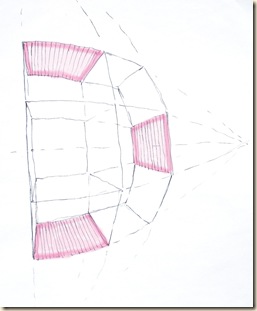
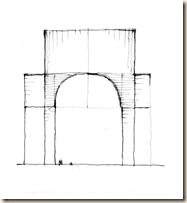
Előre nézve: kereszthajó-oltár.  Feljebb tekintve: kupolatér. Fényképből kettő elég, de rajzoláshoz legalább három normál látókúpot használunk (lásd oldalnézet).

 

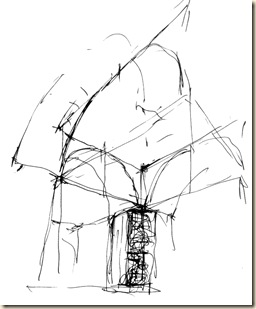
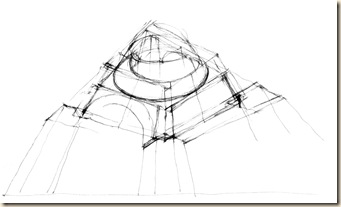
Magassági skála építése a kiterített gömb-szeleten. Választott egységünk a szemközti kereszthajó négyzetes foltjának magassága. A vörös oszlopot ceruzával (kézzel), nyújtott karral befogjuk. Ez lesz a teljes magasság ötöde. Íves mérő-képsíkunkon e mércével lépegetve, ötödszörre érjük el a kupola-belső foltját fentről határoló innenső boltöv peremét.

   

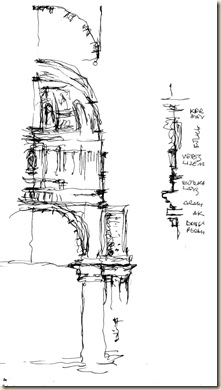
Sávos panoráma szerkezetépítésének fázisai a Bazilikában (lavírozott vázlat tollal).

 

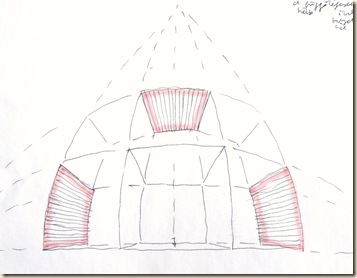
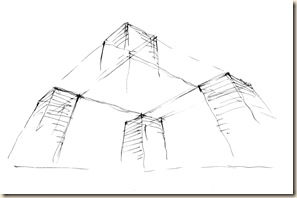
A kupola tambur-palástja: az égtáj-negyedeket szoborfülkék hangsúlyozzák. A fülkék közti sávot három (egyenként két négyzetnyi, téglalap-alakú) lizéna-mező tagolja. A szélső fél-oszlopok erős dőlése a harmadik iránypont helyzetét sejteti valahol fenn, a zeniten.

Az ecsetrajz szerkesztéseinek lépései:

 

A lavírozott tollrajz korábbi tanulságait felhasználva, a magassági skála ötödölésével, szakaszosan készül a közép-sáv. A padlóra kiterített lap alsó és felső peremétől befelé lépegetek. A részletek egymást erősítik.

  

A főbb tónusviszonyokat a helyszínen néhány, tubusból kipréselt,  ujjal elkent fehér folt rögzíti. (A részletes kidolgozás otthoni munka.)

 

Sávos panoráma video-klippen is követhető – a kamera látószögének emelésével a szélső függőlegesek ívesen összehajolnak.

Mandula

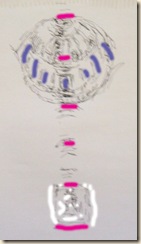
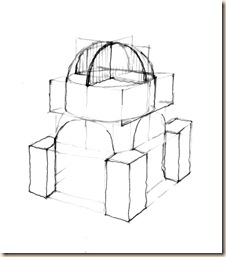
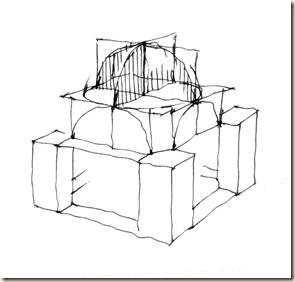
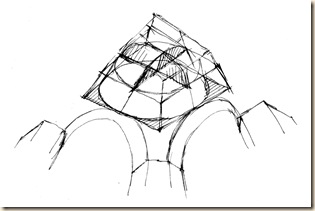
Panoráma-rajzunk talán legkényesebb része a tambur- és kupolabelső (majdnem szimmetrikus görbékkel közrezárt) foltja. Ezt a világos mezőt alsó és felső ívek határolják. Érdemes egyenként tisztáznunk e görbéknek jellegét, mégpedig a befoglaló kockarácsban elfoglalt pozíciójuk szerint!

Szétválasztva az egyes körök ill. kör-darabok érthetőbbek.

   

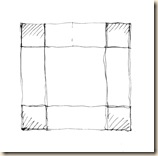
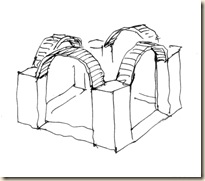
Az alsó ív (a kupolatér, azaz a tambur alapköre) vízszintes síkban elhelyezkedő teljes kör.

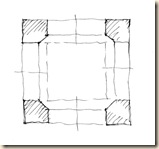
A felső ív (a kereszthajó fejünk fölé tornyosuló boltíve) függőleges síkban futó félkör. Oldalhajóban (az egyszerűség kedvéért a középtengelyen) állva, s felfelé tekintve, a felső ív látszólag belevág az alsó ívbe.

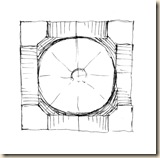
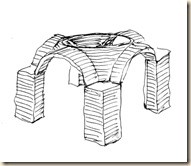
A sémák ideálisan elkülönített kocka-állásokat mutatnak be: talp-kör, oldallap-kör, majd a kettő együtt, végül a takarásos variáció.

Kikereshetjük azt a különleges nézőpontot is, ahonnan a két görbe éppen érinti egymást. Általános példánkban a függőleges síkban futó boltív rátakar a vízszintes síkban futó alapkörre.

Ismét segített rajtunk a kockarács-analógia. A szabadkézi rajzosnak másképpen kell látnia, mint a laikus turistának – a tagozatok egyszerűsítésével, az eltakart formák megjelenítésével, az alakzatok elemzésével szerkeszt.

Kupola-részlet a Bazilika-ecsetrajz vörös alapon c. gouache-ból.

 

Második eset: a Nemzeti Múzeum szabályos lépcsőterének oldal-galériájából egyszerre mutatjuk be a hasáb-szerű tér előttünk, alattunk, felettünk s oldalunkra eső építészeti elemeit. Tekintetünk három-négy-öt normális látókúpot befogva irányul előre, lejjebb, feljebb, oldalvást… Nyakunkat függőleges síkban billegtetjük, vízszintes irányban elforgatjuk.

A látókör kétirányú kiterjesztése részleges panorámát eredményez. Összetett képsíkunk negyed-gömb szeletre hasonlít.

Harmadik eset: teljes panoráma. Nagy tér közepéből előre tekintve, majd oldalvást jobbra-balra, aztán föl-le, nyakunkat négy irányban, két tengely mentén mozgatjuk. Ehhez az előbbi esetek áttükrözésével jutunk el a gyakorlatban. Megvalósulásához olyan központi elhelyezkedés szükséges, ahonnan előre, jobbra, balra, fel és le egyaránt tágas kilátás nyílik (pl. egy plaza galériája).

A látókör minden irányú kiterjesztése teljes panorámát eredményez. Összetett képsíkunk fél-gömb szeletre hasonlít.

Gyakran feltett hallgatói kérdés, hogy hová kerüljenek az iránypontok nagytér-ábrázolási feladatoknál?

Ilyenkor egyetlen lapon a lehető legtöbb térhatároló felület ábrázolandó. Nagy térben állva, szemünk részekből állítja össze a teljes képet. Pillantásunkkal szakaszosan letapogatjuk a falak, a padló, a mennyezet sarkait. Tudatunk különböző látókúpok eredményeiből szerkeszti a panorámát.

Vizsgálódásunk idejére helyettesítsük a látványt befoglaló kockaráccsal!

Minden tárgy és tömeg köré befoglaló kockarács írható. Minden tér kitölthető olyan negatív formával, amire az előző mondat érvényes. Az építészeti szabadkézi rajz egyes fejezeteinél hasznunkra válik, ha a teret négyzethálós nagykocka-belsőként értelmezzük.

A megoldáshoz rakjuk össze a panorámát részeiből! Az egyszerű részleteket hagyományos kocka-helyzetekkel modellezzük.

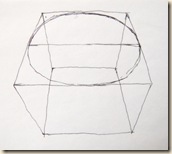
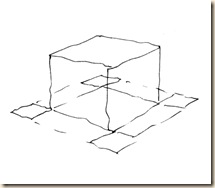
A) Párhuzamos helyzet szemből: egy iránypont.

B) Általános (közel átlós) helyzet két iránypontot eredményez.

Állítsuk be az előbbi hagyományos helyzeteket úgy, hogy a szemközti (A) és az általános, majdnem-átlós-helyzetű (B) kocka összemontírozható legyen, azaz legyen egyik iránypontjuk közös !

A+B) Szemközti és oldalsó helyzet kombinációja. Az eredetileg vízszintes rudak az összemásolt perspektíván törtvonalat mutatnak.

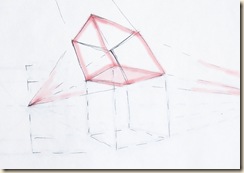
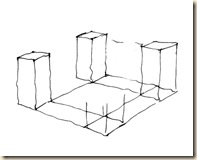
C) Oldalról, alulról nézett kocka-helyzet: három iránypont.

A kockarács további kiterjesztését  (a szokásos átlós módszert alkalmazva) sorolással és tengely-irányú tükrözéssel valósítjuk meg. A törtvonalat mintázó rudak fokozatosan ívekké alakulnak.

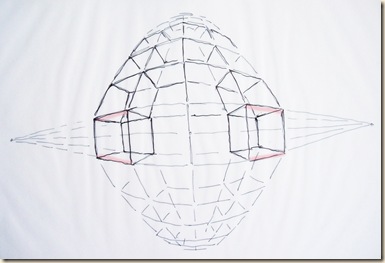
Tükrözéssel létrehozott teljes panoráma. A kezdetben egyenes vonalakkal megrajzolt rész-kockák  panoráma-összességükben íves átrajzolást kívánnak.

A csupa egyenes vonallal operáló, hagyományos perspektíva-elmélet csak egy-egy szokványos látókúpon belül érvényes a kockahálóra.

Összetartás-tapasztalatunk szerint a szélső-ferdék, mint szögszárak által közrefogott köztes ferdék nyalábja egy-egy távoli szög-csúcs - mint iránypont - felé mutat.

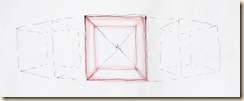
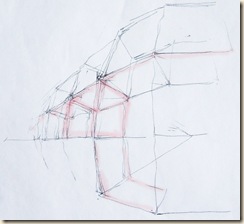
A+B) Oldalirányba bővített kockaháló görbülő élei

Tudatunk elismeri, hogy pl. a nagykép szélein lévő, azonos magasságban s térbeli mélységben lévő (eredetileg vízszintes) elemek összetartoznak, hiszen középen lévő társuk révén kapcsolódnak. Előre nézve előbb így (vízszintesnek), oldalt nézve viszont utóbb úgy (ferdének) láttuk őket. A két eredmény sehogyan sem esik egy vonalba!

Amikor tekintetünkkel széltében-hosszában végigpásztázzuk a panorámát, azaz mezőről mezőre araszolunk, rajzunkon csak úgy tudjuk összeróni a látókúpokat, hogy a hagyományos kockarács éleit meggörbítjük.

A+B+C) Oldalvást majd fokozatosan felfelé bővítjük látóterünket. Egymáshoz kapcsolódó kockák segítségével következtethetünk az iránypontok helyzetére. Az élek inkább ívesek, mint egyenesek. Aki minden áron mindent látni akar, mondjon le az egyenesekről! Az ábra fejre állítva a mélybe tekintést modellezi. Szerkesztésnél a hátsó négyzetlapok hihetőségére törekedjünk!

D) A fentiek tükrözése. Ha elég nagy a papír, és hajlandók vagyunk meghajlítani a kockarács egyeneseit, a valóság párhuzamosai belekényszeríthetők a vonatkozó iránypontok fókuszába.

E) Az előző eset forgatása. Kockahálónkat fokozatosan bővítjük: előre, oldalt, felfelé és (tükrözéssel) lefelé is. A tompaszögű szakaszok ívvé hajolnak.

Miközben a rajzon folyamatos vonallá próbáljuk összevonni a korábbi rész-megfigyelések törtvonalú szakaszait, megbizonyosodunk arról, hogy ezek csak ívvel hozhatók össze. Még a központi kocka-elemen is kimutatható enyhe görbület az utólagos átrajzolásnál .

A végső összetartások óriáshorizonttal szakaszosan ellenőrizhetők.

F) Az előző helyzet újabb tükrözése. Teljes panoráma modellezése kockaráccsal

Kísérleti példánkban a látómezők összetoldásakor (továbbá a tükrözéseknél esedékes átrajzolás alkalmával) rendre megbizonyosodhattunk arról, hogy a rácsozat csomópontjaihoz tartozó tompaszögek finom ívbe simulnak. Azonos rúdhoz tartozó szélső szakaszok csak így köthetők össze.

Összefoglalás

Forgassa nyakát, ki hasábban állva minden térfalat látni akar! Amikor látókörünket a teljes kockahálóra kiterjesztjük, az egyes kockákat képtelenség tisztán egyenes szakaszokkal ábrázolni. Látómezők összetoldásakor a befoglaló kockarács törtvonalú szakaszai ívekhez simulnak. Az iránypontok helyére az egyes rész-kockák elkülönített elemzéséből következtethetünk.

Kupola-tér

A Bazilika kupolaterének röntgen-rajza.

Nem könnyű a nagytér egyszerűsített szerkezeti rajzát elkészíteni. Vonatkoztassunk el átmenetileg az egyetlen nézőponthoz kötött látványtól, amely általában szokványos, fotó-realisztikus képkivágást nyújt, s ne törődjünk egyelőre a sok díszítéssel se!

A hagyományos (két iránypontos) látásmódot illusztráló pasztell-kép rajzolási sorrendje MB honlapján szereplő Bazilika című füzet leírása szerint filmszerűen is végigkövethető.

Három iránypontos helyszíni vázlat. A virtuális nagykocka méreteit kutatva, a sarokpillér átlósan lecsapott oldalával szinte szemben állunk. Ez az úgynevezett vezérsík, rajzunk megbízható kezdő-skálája, melyről a részlet-osztások derékszögű hálója szinte torzulás-mentesen vehető át.

Sarokpillér átlósan lecsapott oldalával szemben állva.

Mindenek előtt tisztázzuk magunknak az építmény átlátszó építőkockákból kirakható vázát!

A központi kupola-tér szerkezetének megértése céljából sétáljuk körül a kereszthajós csarnokot, s tanulmányozzuk az elsőrendű (térhatároló, teherhordó) elemeket! A másodlagos, díszítő formák ebben a stádiumban figyelmen kívül hagyhatók.

Ha a főtemplom kupola-terét kívülről s felülről, kicsinyített makettként képzeljük magunk elé, könnyebb lesz annak belülről, alacsony horizonttal való térbeli ábrázolása.

Az építés valós folyamatának képzeletbeli modellezése szintén az enteriőr felvázolását segíti elő.

Virtuális nagykockát magyarázó szerkezeti vázlatok – belső kép, alaprajz és madártávlati modell.

A belső tér szélességi és magasság viszonyainak eredeti arányait tengelyirányokból nézve érdemes mérlegelnünk.

Tengelyirányú főhajó-nézetek (előre, hátra).

Az oszlop-párokkal szembefordulva, a látványra virtuális négyzethálót illesztünk.

A szerkezeti rács alapegysége legyen a főméretek legnagyobb közös osztója! Itt pl. a sarok-pillérek nyílásközével dolgozhatunk.

Alkalmas kiindulásnak tűnik a szimmetrikus csarnoktérbe írható virtuális nagykocka, amely a kupola alatti felmenő szerkezetek közé szorítható.

Az előkészítő gyakorlat során fontos szerephez jutnak vetületi vázlataink, melyeken az egyszerűsített építészeti alkotóelemek kockahálóhoz való viszonyát rögzítjük.

Az alaprajz értelmezésének lépései. Belső kocka alapnégyzete, sarokpillérek másod-négyzete, átlós lesarkítások, kupola vetülete.

Ilyen előtanulmányok után végre hozzáfoghatunk a “Tér mint nagykocka-belső” felfogásban készítendő perspektívánkhoz.

 

A központi kupola-térbe képzelt virtuális nagykocka alaprajzból származtatott tengely-nézetei. Jól látható a sarokpillér vállaira ültetett donga és a kupola közti léptékváltás. A kupola alapkörének sugara egy harmaddal nagyobb, mint a pillérlábakhoz tartozó félkör-ív. A valós kupola belseje nyújtottabb. Alaprajz, nézet (metszet) a térbe írható nagykocka arányai miatt szükségesek.

A hatalmas belmagasság miatt horizontunk a padlót súrolja. Számolni kell harmadik irányponttal is, amely felé a terpesztett nagykocka összehajló függőlegesei mutatnak.

 

A pillérvastagság egyelőre becsült érték – a térbe írható kocka oldalaránya összehasonlítandó a donga-vastagsággal. A rajz közepén húzódó függőlegesek nagyjából párhuzamosak maradnak a lap szélével. A gazdag építészeti tagozatok ebben a fázisban összevonhatók.

A kettős négyzetet (a távoli iránypontok feltételezett ismeretében) a sarokpillérek felső síkjában vázoljuk fel. Ha értjük az alaprajzot és a metszetet, nem tévedünk el a távlati kép magjának szerkezeti felépítésében.

A közeli pillérlábat - kontúrjaival ábrázolva - eleinte átlátszónak mutatjuk. Vázolás közben folyamatosan ellenőrizendő a kiindulásul választott belső kocka hihetősége. Az eleinte sallangmentesen kezelt tiszta formákat utólag részletezzük. Az előtérben fokozatosan visszaállítjuk a lizénák, tagozatok, párkányok változatos anyag-, forma- és szín-világát.

Akkor sikerül perspektívában az ellipszis, ha megtaláljuk az alapkör köré írható teljes négyzetet! A befoglaló négyzet megalkotásához szükség lesz a donga-ívek felső felezőpontjaira.

   

Belső röntgen-rajz feltételezi, hogy képesek vagyunk alacsony horizonttal, fölénk magasodó kockát bármelyik alaphelyzetben rajzolni.

Ne feledjük, a hatalmas belmagasság miatt gyakorlatilag padló-horizonttal van dolgunk!

A fedlapon dolgozva, a sarkok átlós kiterjesztésével megbecsüljük a pillérek vastagságát – így készül a külső négyzet-gyűrű.

Pillérek lesarkítása, alulról nézett rövidülésben. A négyzet-keresztmetszetű hasábok belső sarkai átlósan le vannak csapva, így közelítik meg a centrális formát.

A bolt-vállakra félköríveket emelünk. Előbb a belső, függőleges síkon dolgozunk, majd a donga-mennyezet félhenger-palástját behatárolva, a hátsó síkon duplázunk. Perspektívában a félkör javasolt rajzolási sorrendje: vonórúd (átmérő), külső érintő, magasság (sugár), befoglaló iker-négyzet, negyedekből összerótt félkör-ív.

A kupolát tartó tambur alapkörének befoglaló négyzete oldalfelezői révén a belső donga-ívekre támaszkodik. A tambur felső körét szintén befoglaló négyzete segítségével rajzoljuk meg. Innen indul a kupola alapköre.

A kupola-félgömb összehajló gerezdjei az égtáj-metszékek közt kialakuló mezők arányos tovább-osztása révén jönnek létre. Az égtáj-tengelykeresztre iker négyzeteket állítunk. A félköríveket negyedekből rójuk össze. A félgömb kontúrját burkológörbe szolgáltatja.

Kupola-metszet vázlata. A sávokat szín szerint megkülönböztetve készül az előtanulmány. Tengelyirányban haladunk. A tambur rajzolása közben mérőegységként használhatjuk az aranyszínű korinthoszi oszlopfőt. Az arany sávot háromszor véve a donga-vastagságot kapjuk meg.

Nem ússzuk meg számolás nélkül: a donga-bélés gazdag díszítéseit méricskélve tudatosítjuk, hogy a félkörív feléhez (azaz egy negyednyi palásthoz) nyolc darab kettős (egyenként nyolcszög-alakú) kazetta tartozik.

A konzolos alapkör korong-vastagsága beforgatott metszetként rögzíthető. Drapp, arany, vörös – mondogatjuk szín szerint.

A tambur függőleges tagolása, lentről felfelé a következő: dongaperem, alapkör-tagozata, aranyozott konzolsor, szürkés lábazat, vörös lizéna (benne szoborfülke az égtáj-kereszt hangsúlyozására ill. három-három kazettás lizéna-köz), fent korinthoszi oszlopfő-sáv és a záró-tagozat pereme. Felette drapp-színű a kiugró párkány.

A belső, virtuális nagykocka - szemből négyzetesnek látszó homloklapja – tehát a lenti padsorok felső pereméig mérve tűnik érvényesnek.

A kupola alatti henger (tambur) lizéna-közeinek leszámlálását megkönnyíti az égtáj-negyedeket kihangsúlyozó falfülkék felismerése. Minden tengelykereszthez tartozik egy szoborfülke tartozik.

A negyed-határoló szobrok között három-három lizéna-köz tagolja a henger belső palástját. Amikor az alaprajzban megértett körcikk-osztásokat átvetítjük a nézetre, kiadódnak a rövidülések.

Aki metszetben sikeres, távlatban is sikeres!

A tambur hengerpalástjának kazettás lizéna-köze. A féloszlopok közébe írt intarziás kazetta aránya két négyzetnyi. A konzolos alapkör sávjának teljes vastagsága  szintén egységnyinek vehető.

A lentről szemlélt kupola formája nyújtott félgömbnek tűnik. A szabályostól való eltérésének mértékét a szemből látott cikkely színes részleteinek pontos megfigyelésével dokumentálhatjuk.

Ebben a fázisban is a hiányok (kitakarások) feltérképezése többet segít, mint a látható formák lejegyzése.

Kupolagerezd vázlata. A cikkelyek irányába fordulva, egy-egy gerezd belső rajzolatának valós arányával ismerkedünk meg. A szabályos félgömbtől való eltérés mértékére a mintázatból is következtetéseket vonhatunk le.