Teraszos torony

Másodéves feladat (Vertikális kompozíció, kötött maggal, alacsony horizonttal)

Részleges beállítás szögletes váztestekből

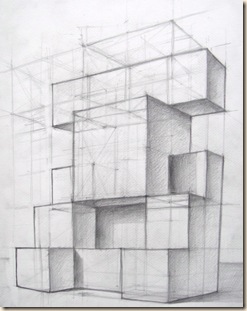
A szimmetrikus építmény központi magja minden tankör számára közös: két és fél váz-kockából összerakott torony.

Láthatatlan alátét-kockával középen és  két fél-kockával a szárnyakon csoportunk elegánsan megoldja a tornyos beállítást, a normál padlószinten állva. Ez a a gólyaláb-módszer.

Kiegészítő elemeink: üres és teli kockák ill. hasábok (kockasorok), melyek pontos elrendezését szintenként alaprajzok és égtájakról elnevezett homlokzatok (vízszintes és függőleges metszetek) tisztázzák.

A legfelső szintet híd-szerű képződmény alkotja.

A könnyebb tájékozódás kedvéért a vetületeket betűkkel és számokkal jelzett modulhálóra visszük fel. A magasságokat római számok (szintek) mutatják.

A táblai ábra-sor. Az alaprajzok sraffozott része a belső tömeget, vonalas része a felülről látható alsóbb teraszokat mutatja. A belső magot következetesen pirossal jelöljük meg! Azonos színhasználat saját tájékozódásunkat segíti.

A puding próbája az evés! Alálátás-csúszó-pont demonstráció a VI-os teremben. A legfelső váz-fél-kocka rúdmetszeteinek tárgyilagos ellenőrzése - létra segítségével. (A létrán a szerző látható.)

Az első csúszópont-gyakorlat a színes jelölő-drót kiválasztásával kezdődik. A kísérleti drót-nyalábbal diák kínál diákot.

 A demonstráció játékos előhangjának tekinthető szín-választás szimbolikus: ezzel mottónkat erősítjük . (“Minden nézőponthoz egyéni perspektivikus torzulás tartozik!”)

A rajz-helyről megbecsült M-értéket (alálátás esetén: létra segítségével) a központi kockatorony közeli függőleges élén csúszó-pontként rögzítjük.

A beállított tárgy kézzelfogható megjelölése után visszaülünk helyünkre, s eredeti nézőpontunkból újra szemügyre vesszük a váztest nevezetes rúdjainak látszólagos összemetsződését.

Hiba esetén megkeressük az elrajzoláshoz rendelhető nézőpontot.

Metz Ádám részben tónusozott tornya.

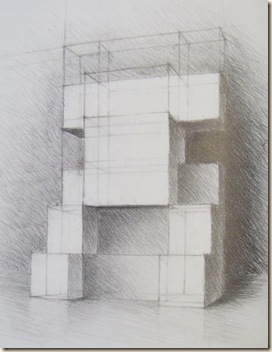
Miklós Zita tisztán vonalas megoldása.

Hertel Anna finoman tónusozott rajza, vetett árnyékos háttérrel kitöltve.

Füzes Bálint Péter játékos tovább-építése, tükröződő előtérrel.

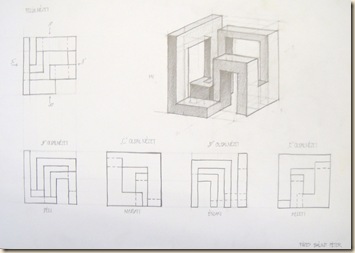
Második feladatunk vetület-helyreállítási rejtvényének egyik megoldása szintén az ő kezét dicséri:

Három iránypontos horizontális kockasor összetartásait az Óriáshorizont (vagy: Égtájmappa) módszerrel ellenőrizzük.

…”A köztes ferdék a szélső ferdék közé szorítandók. Az iránypontok ismeretében (kézben tartott gumizsinórral vagy a vizsgált sarkok gombostűre való tűzésével) csoportosan ellenőrizhető valamennyi köztes ferde-nyaláb.”

Borító minta:

A rajzokat szabványos borítóba tegyük, feliratozás vastag, vágott végű filctollal történjék. (Hasonló eredményt érhetünk el, ha a két vonalas, függőleges betű-szárak közét utólag kitöltjük.)

Emlékeztetőül: az első házi feladat MB honlapján található (Képes Kockatan, 10. ábra)!

Aula tér-analízis

Az egy iránypontos folyosó-rajz után kitágítjuk látóterünket, s a derékszögű aula-körüli oldalfolyosókat egyetlen, széles-vásznú lapon próbáljuk ábrázolni.

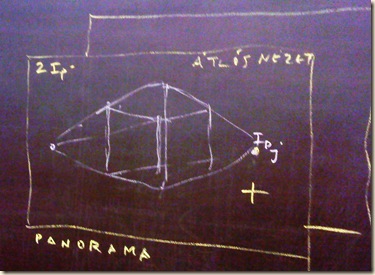
Három látókúpot dolgozunk (spekulatív módon) össze: egy iránypontos folyosó balról, másik folyosó jobbról, két iránypontos sarokpillér középen, átlós nézetben… összemásolva (egymásra csúsztatva) a szomszédos iránypontok lassan kialakul a panoráma szerkezete. A horizonttól távoli vízszintesek (szélső ferdék) közös ívre feszülnek. (Korábban tompaszögeket zártak be.)

A táblai magyarázat fotóit Oltványi Tamás készítette.

A nézőpontok összemásolása egy-egy cél-kocka bevetésével szemléltethető. (A vonatkozó elméletet l. a Bazilikáról szóló “Panoráma bővített kockaráccsal” című írásomban.)

Az átlós nézet a képmező közepét elfoglaló sarokpillérre vonatkozik. Ennek a szélső iránypontjait hozzuk fedésbe az oldalfolyosók saját (eredetileg egyetlen) enyészpontjával. Ezt a műveletet mutatják az egymásra helyezett lapok. (A kulcs-szavak magyarázatát a Tükröződő toronytrióban kereshetjük vissza.)

Megoldás: az ív.

Előtérben szerepeljen a padló-háló is!

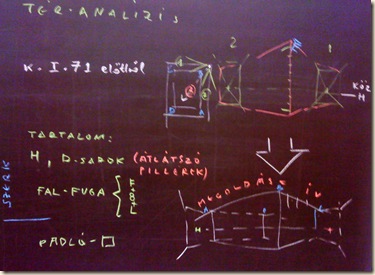
A beadandó rajz tartalmazza: a horizontot (ahol a cikk-cakk kiegyenesedik…) az átlátszónak ábrázolt pillérek mögötti aula-sarkokat (a D jelű kocka-élet) és a közeli fal-fúgákat!

A táblai rajzon szerepel az aula alaprajzi elrendezése is: három irányba kell néznünk egyszerre. A három perspektívát szélső ívekkel simíthatjuk egy szerkezetbe. Ne feledjük: egyetlen vízszintesünk: a horizont összefogja az egész panorámát!