Képzelt belső terek megjelenítése
Forgástestek kívül, belül.
Tömeg és tér viszonya - léptékváltással. Tárgyrajz és térrajz kapcsolata. Pozitív és negatív formák. Gömb, henger, kúp, gégecső példája. Egyszerű formák álló és fekvő változatainak elemzése. Tisztavonalas, felületosztásos és tónusos grafikai megoldások.
A szeletelő módszer

Minden a PHV-kockával kezdődik.
Végtelenítsük a “beülő hasábot” (l. Folyosórajz)! Alkalmazzunk befoglaló kockarácsot, vetületi négyzethálókat, találjuk meg a nézőpontunkhoz tartozó horizontot és az iránypontot, határozzuk meg az első kocka virtuális mélységét, vigyük fel minden előállított felületre a méter-osztásokat, átlókkal keressük meg a szerkezeti kockarács csomópontjait, szerkesszünk a legtágasabb mozaikokban, fejezzük ki rövidülő-összetartó háló-osztásokkal a térhatároló síkokat , a hálótól való eltéréseket rögzítsük először a vetületeken...
Segédlet "Az én barlangom" c. elsőéves modellfeladat rajzi feldolgozásához
Kulcs-szavak: alaprajzi háló, átlós módszer (saroktükrözés), befoglaló (beírható) kockarács, beülő hasáb (végtelenített, négyzet-keresztmetszetű folyosó), elő-tónus (felületosztás, anyagjelölés), esésvonal, helyi kontraszt, iránypont-koordináták, képkivágás, képsík-mozaik, lamella-koordináta, metszet-profil, méter-háló, négyzethálós nagyítás, PHV-kocka, rácspont, rész-kontúr, rétegvonal, síkra-bontás, szeletelő módszer, vetület, vezérsík.
FELADAT: Tömör kockába üreget mélyítünk. Ábrázoljuk a képzeletbeli barlangunkban feltáruló tér látványát!


Kúp-szerű tér belseje. Fent a vetületek, lent a térsarok-lapjaival párhuzamos kúp-metszetek sorakoznak. Az enteriőr ábrázolást úgy készítjük elő, hogy a (kockából kivágott) belső teret vázlatosan, modell-szerű tömegként kívülről ábrázoljuk. A modellre fokozatosan felvisszük a belső tér ábrázolásához szükséges lamella-rendszert. Minél bonyolultabb a belső tér, annál több metszet-sorozatra lesz szükségünk.

A téma egy ókori barlangsír tisztavonalas távlati képére emlékeztet, amelyet rakott kősorok és a padlóháló osztásai érzékeltetnek.

Atreusz király kincsesháza, Mykene-ben (tholosz).
Intuitív (azaz kitalált) belső terek grafikai megjelenítése az alábbi előzmények feltételezett ismeretére épül :
Folyosórajz (hosszúkás, szimmetrikus tér legalább egy iránypontos perspektívában való, természet utáni rajzolása), mely átmenetet képez a tárgyrajz és a térrajz között;
Tónustan (a vonalperspektívával elérhető mélységi hatás fény-árnyékos fokozása, átmenetek képzése ceruzával, természet utáni tárgyrajzolás)
PHV (perspektíva helyreállítása vetületekből)
elnevezésű szerkesztéses feladat-típus megoldási folyamatának elsajátítása, amely a befoglaló kockarács használatát tanítja;

Félgömb-szerű kupolatér bordás makettja
Tárgyrajztól a térrajzig
Tárgyrajz és térrajz közt léptékváltás a határ. Térrajz során a téma és a szemlélő viszonya megváltozik. A kiskocka megnő, a horizont lesüllyed (l. MB: Folyosórajz).
Szabadkézi rajzban a Tér négyzethálós nagykocka-belsőként értelmezendő (l. MB: Fókuszban a Térsarok).


Szalag-szerű folyosó távlati képe. Négyzethálós vetületek és befoglaló kockarácsos modellrajz
segítségével készült.
Befoglaló kockarács
Bármilyen bonyolult alakzat megjelenítésére alkalmas a befoglaló (burkoló) kockarács. Akár pozitív, akár negatív formát kívánunk perspektívában bemutatni, a formációra kívül-belül szorosan illeszkedő kockarács (ami vetületekben négyzethálót jelent) mindig kisegít minket.
A köztes részletek a hálón belüli osztások fokozatos sűrítésével fejezhetők ki. Ez a gyakorlatban további (az előzőkre merőleges) szeletelést, azaz (rajzilag) csíkozást jelent. Szabadkézi rajzban a fokozatosság fogalma alatt a korábbi háló-osztások perspektívában megvalósítandó felezését (negyedelését, nyolcadolását, tizenhatodolását, harminckettedelését…) értjük.
A végleges fény-árnyék-hatásokat befejező tónus-rétegekkel érhetjük el.
Térbeli alakzatokat síklapok vagy görbe felületek határolnak. Az íveket húrokkal vagy érintőkkel, a görbe felületeket átmenetileg síkokkal helyettesítjük.
Pozitív formára befoglaló kockarácsot borítunk. Negatív formánál beírható kockarácsot alkalmazunk: barlangunk üregét kibéleljük.

Befoglaló kocka modellje

Lamellás doboz kivett lamellával

Hossz- és harántlamellák
Bújjunk bele a dobozba!
Rajztudásunk eddig valós tárgyak megfigyelésen alapuló, természet-hű ábrázolásán nevelődött. Ez a feladat arra a feltételezésre épül, hogy a magunk elé képzelt szerkezeti váz-kockát képesek vagyunk akár fejből is megrajzolni. Pozitív formák szerkezetét befoglaló kockaráccsal, burkoló négyzethálóval közelítjük meg.
A tömör nagykockából kivájt tömeg-hiány az elképzelt léptékváltás absztrakciója során belső térré alakul. Barlangunk belsejének megrajzolása nem könnyű feladat. Próbáljuk a negatív formákat is határoló felületeikkel megjeleníteni!
Első lépésként (mondjuk képsíkunkkal párhuzamosan) egyenlő vastag lamellákra daraboljuk a befoglaló nagykocka tömegét. Ez néhány jellegzetes metszetet (oldalnézetet, falnézetet) jelent. Egyszerű barlang-profil és szerencsésen kiválasztott nézőpont esetében egy sorozat lamella elegendő.
Bonyolult képződmény esetén az előző sorozatra merőleges irányba sorakozó lamellákra is szükségünk lesz. Lamelláink a szeletelő (kazettás) módszerrel képződnek: a vízszintes alaprajzi hálóra (a padlóra) függőleges és egymásra is merőleges síklapok sorozatait állítjuk.
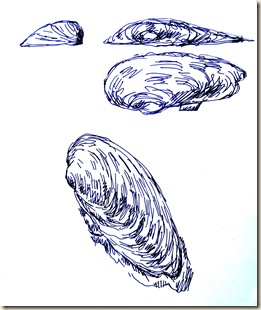
Dunai kagyló nézetei
Az imént leírt lamella-formáció háztartásunk jégkocka-tartó rekeszeire hasonlít. Konyhai példánál maradva, idézhetjük a sok-húros tojás-szeletelőt is!

Tojás szeletelő kézben tartva – a lamellás módszer ötlete

Kemény tojás szeletei széthúzva – illusztráció a kazettás módszerhez

Tisztavonalas tojás-belső. Zeppelin-testére emlékeztető látványát (képsíkunkkal párhuzamos) tojás-szeletek perspektivikus sorozata alkotja.
Réteges formák után kutatva, környezetünk számos mintát szolgáltat: bizonyos geológiai képződmények (ahogy a mészkőréteg kialakult), vagy a dunai kagyló recézett felülete.
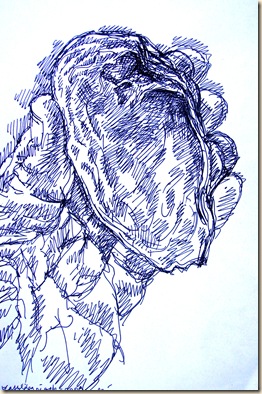
Kézben tartott dunai kagyló, toll, 2008 Lamella-tan
Hogyan ábrázoljuk perspektívában a felnagyított lamellát? A magassági osztásokkal ellátott, közeli függőleges éllel kezdjük. Bejelöljük a horizontot és az iránypontot. Ezután következhet a lamella négyzethálója. A magassági osztásokat rendre összekötjük az irányponttal. A szélső ferdék, majd a köztes ferdék plasztikusan kirajzolják lamellánk térbeli helyzetét. Az egyes mezőkhöz tartozó rész-kontúrok torzulását - a háló-mezők látszólagos deformációjához igazodva – a perspektíva szabályai szerint felvisszük a lamellára. Eközben a közeli rész-mezőket kinagyítjuk.

Lamella szemből

Lamella rövidülésben

Keresztirányú lamellák skurcban
A kockán belüli nevezetes pontokat lamella-koordinátákkal határozzuk meg. Eljárásunk lépéseit a függő cseppkő térbeli helyzetének meghatározásával szemléltetjük:

Cseppkő-koordináták
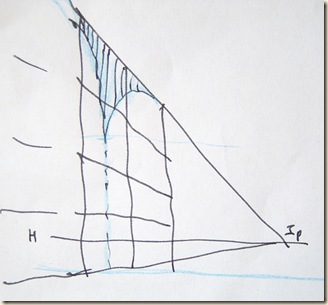
Cseppkő-lamella rövidülésben
1) A padlósík alaprajzi hálóján bejelöljük a csepp helyét (Px-y) és nézőpontunkat (NPx-y).
2) A képsíkunkra merőleges hosszanti lamellán bejelöljük a csepp magassági helyzetét (Py) és a nézőpontunkhoz tartozó szemmagasságot (NPy). Ez a lamella szállítja perspektívánkhoz az erős rövidülés adatait.
3) Haránt-lamella – Ha további jelentős információra lenne igényünk, akkor a képsíkkal párhuzamos metszeteket is hasznosíthatjuk a látvány szerkesztésénél.
Egy-egy négyzethálós lemezt érdemes előbb nézetében kiterítve tanulmányoznunk.
Boglya (félgömb) példája
Állapítsuk meg a térhatároló kontúrvonal jellegzetes töréspontjainak hálóhoz viszonyított koordinátáit! A metszet-kontúrok látványtervünkön rövidülésben jelennek meg. Szeletről szeletre haladva, az esésvonalak csíkjai lassan kirajzolják a barlang belső felületét.
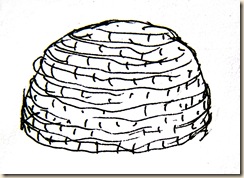
Falazott boglya – rétegvonalakkal

Szeletelt boglya – esésvonalakkal

Félbevágott boglya – falazott felületosztással

Félgömb belsejének vetületekből való szerkesztése

Félgömb (bordás) belseje – esésvonalakkal
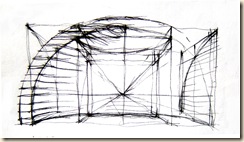
Félgömb (falazott) belseje – rétegvonalakkal

Félgömb vetületei (a fenti rajz részlete)
Legtöbb adatot a szélső lamellák szállítják. A nézőpontunkhoz tartozó hosszanti lamella éppen élben látszik. Ezen a vonatkozó tér-profil jellegzetes töréspontjainak magassági koordinátái gyűjthetők össze. Minél összetettebb a belső térre tapadó négyzethálós felület, annál sűrűbb szeletelésre lesz szükségünk egy-egy főirányban.
Az ábrázolandó alakzat kiterjedése és bonyolultsága határozza meg a lamellák számát és jellegét. Több sorozat esetén színek, betűk, számozott jelek használata nagyon ajánlatos.
A vizsgálandó lamellán a teljes tér-metszet felvitele után helyezzük el választott nézőpontunkat és a horizontot is! Ekkora már kiderül, hogy nem lesz szükségünk a hátunk mögé eső részletre. Lamellánként mezőről-mezőre haladva, perspektívában rögzítjük a látómezőnkbe eső tér-kontúrt.
A teljes határoló tér-burok látványa a szeletek által szállított rész-kontúrok azonos alaprajzi pontjaihoz (az alaphálóhoz) tartozó magassági pontok haránt irányú összekötésével rajzolódik ki. Ez a kivitelezés gyakorlatában azt jelenti, hogy képsíkunkkal párhuzamosan haladva, keresztirányban “bedeszkázzuk” a magassági állványzatot.
Esésvonal, rétegvonal
Ábrázolandó felületek képsíkhoz viszonyított helyzetének legtakarékosabb kifejezését - a tónusozás előtt - grafikus csíkozással valósíthatjuk meg. Ez közelebbről rétegvonalozást vagy esésvonalozást jelent . A rétegvonalozás egyenletesen rakott, vízszintes téglasorokkal szemléltethető. Esésvonalakra példa a deszka falburkolat, vagy tetőn a fémlemez-fedés illesztéseinél alkalmazott korcok rajzolata. Az esésvonal irányára a legrövidebb úton legördülő vízcsepp utal.
Milyen lehetett a trójai faló belseje?


Így kucoroghatott a tíz válogatott görög harcos a trójai faló belsejében. A hajóépítésben is járatos, leleményes Odüsszeusz hosszanti irányban valószínűleg deszkákkal borította a keresztirányú bordákból megformált paripa testét. A legendás lónak szilárd lábakon kellett nyugodnia, hogy kibírja a vontatást is. Lábanként legkevesebb három rúddal számolva, könnyen elképzelhetjük, hogy a has szűk terét átlósan benyúló merevítések gerendái tovább csökkenthették.
ÖSSZEFOGLALÁS
Pozitív és negatív formák szerkezeti rajzát befoglaló kockaráccsal vagy burkoló négyzethálóval közelítjük meg. A nagykockán belüli nevezetes pontokat lamella-koordinátákkal határozzuk meg. Lamelláink a kazettás módszerrel képződnek: a padló-hálóra egymásra merőleges pengefal-sorozatokat állítunk. Lamellánként haladva, perspektívában rögzítjük a látómezőnkbe eső tér-kontúrt. A teljes tér-burok látványa rész-kontúrok keresztirányú összekötésével rajzolódik ki. A végleges fény-árnyék-hatásokat befejező tónus-rétegekkel érhetjük el.
Minden spekulációnál többet ér a terek és tónusok türelmes megfigyelése. Rajzoljunk minél többet természet után!
Íves felületeken a tónus-pászmák alkotó-irányúak.
MB-hivatkozások :
Folyosórajz
Perspektíva Helyreállítása Vetületekből (PHV)
Első kocka – szélső kocka (a Papírcsík-módszer)
Térsarok kockatoronnyal
Ceruzatechnika
Lamellák
Tárgyrajz
Térrajz
Tónus-tan






























 Attila múzeuma.
Attila múzeuma.  Alexandra sarka.
Alexandra sarka.  Tamás színháza.
Tamás színháza. 





























