Kulcs-szavak: befoglaló kockarács, centrális projekció (perspektíva), felezősík (segédvetület), képpont, képtávolság, papírcsík-módszer, szélső (köztes) ferde, tárgyképsík, tárgypont, térsarok, vezérsugár.
Gyakran feltett hallgatói kérdés, hogy a perspektíva helyreállítása vetületekből (PHV)-típusú szabadkézi szerkesztéses feladatoknál hová kerüljenek az iránypontok?
Különösen kényes ez a téma a függőlegesek összetartása esetében. Erős alálátásnál előre rögzített oldalsó iránypontok típushibának számítanak. Ebből ugyanis a felső régiókban hajóorr-szerű, hegyes-szögűnek látszó oldallap-állások adódnak, azaz a befoglaló kockarács derékszögei már a kiindulásnál deformálódnak. Iránypontok korai (többnyire túl közeli) kitűzéséből általában túl kicsi tárgy-méret következik.
Az iránypontok száma képsíkunk és a téma homlokfala közti viszonytól függ (l. MB: Tükröződő Toronytrió).
Ha a Teret képviselő négyzethálós nagykockát kifordítjuk, térsarokhoz jutunk. Térsarokkal magyarázva, annyi iránypontunk lesz, ahány lapját képsíkunk elmetszi. Tekintetünket megbillentve, képsíkunk a térsarok mindhárom négyzethálós lapját metszi: három irányponttal kell számolnunk (l. MB: Fókuszban a térsarok).
Harmadik irányponttal akkor találkozunk, amikor közelebb megyünk az ábrázolandó tárgyat vagy teret befoglaló kockarácshoz. Tapasztalatból ismeretes, hogy kb. két-és-félszeres tárgymérettel azonos képtávolságnál van a két iránypontos és a három iránypontos esetek közti határ. Innen nézve a szélső kocka eredeti magassága és annak tárgyképsíkon felfogott vetülete közti különbség még elhanyagolható, azaz a függőleges szakaszok még nem torzulnak. Állításunkat oldalnézeti segédvetület igazolja. Ennél kisebb képtávolságnál belép a harmadik iránypont.
Három iránypontos szerkesztés az égtáj-mappával, 2009, szept. 29-én (BME K. ép. III. IV. terem)
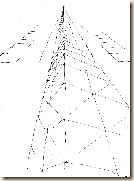
Nézzük kockatornyunkat olyan messziről, hogy mindhárom iránypont ráférjen rajzunkra! Másképpen fogalmazva: rajzoljunk nagyon kicsi tornyot! Nevezzük el a baloldali iránypont felé futó összetartásokat (épület-szerkezetre gondolva: födémperemeket) B, ill. a jobboldali iránypont felé futó összetartásokat J-vel!
Lentről felfelé haladtunkban a közeli kocka-élnél formálódó BJ-sarok szög-változását elemezzük. Általános helyzetű (azaz se nem párhuzamos, se nem átlós, l. „Tükröződő Toronytrió”) kockatorony esetében is találunk olyan szintet, ahol B és J éppen derékszöget alkotva fut össze. Felette hegyesebb, alatta laposabb az átellenes szélső ferdék által bezárt sarok-csúcs. A teljes él-hossz valójában csak több látókúpba fér el.
Oldalnézet értelmezi, hogy a tornyot közelről szemlélve, szakaszosan tapogatjuk le látványát. Mindegyik „odapillantáshoz” újabb vezérsugár, s ahhoz arra merőleges tárgyképsík tartozik.
Kockatorony több látókúppal
Vizsgáljuk tornyunkat szintenként! Horizontunktól távolodva, az emelet-magasság (az egységnyi kocka-él mint átfogó) egyre inkább eltér annak nézőpontunkból rövidülésben látott vetületétől (mint befogótól). Ez a magyarázata annak, hogy a kockatornyot magasítva (közeli nézőpontból, felfelé tekintve) még a függőlegesnek maradó központi él emelet-osztásai is rövidülnek. A szélső kontúr-szakaszok szakaszosan befelé hajlanak, azaz az eredeti függőlegesek többsége összetartónak látszik.
ANALÓGIA ELSŐ ÉS HARMADIK IRÁNYPONT KÖZÖTT
Utcán sétálva, szokványos szemmagasságból, a négyzethálós járda-mintát (párhuzamos helyzetben), egy iránypontos perspektívában látjuk (l. Tükröződő Toronytrió). Az összetartás-rövidülés geometriáját oldalnézetben szemléletesen magyarázható.
Horizontális és vertikális helyzet - a látvány ugyanaz!
A horizontális helyzetet olyan végtelenített kockasor jeleníti meg, ahol a szemlélő magassága éppen kockányi, képsíkja valamelyik szemközti kocka-oldal, látványa pedig az ezen összegyűjtött távolabbi kocka-sarkok összessége. Emlékezzünk arra, hogy a perspektíva: geometria (centrális projekció). Képpontokat úgy kapunk, hogy a tárgy-pontokat rendre összekötjük a szemünkkel (mint centrummal). Ahol a nézősugár átdöfi a képsíkot, ott lesz a képpont. Most menjünk közel egy felhőkarcolóhoz! Tekintsünk fel annak szabályos négyzethálós homlokzatára! Az előbbi helyzethez képest 90 fokkal elfordított arccal a szemlélő ugyanezt látja, mint az imént.
Bebillentett padlóháló-szeletek révén három iránypontos perspektívához jutunk (Kockatorony sarka alulról nézve)
A vertikális helyzet ekkor olyan talpára állított, a felhőkarcoló oldalának támaszkodó, végtelenített kockasorral magyarázható, ahol a hanyattfekvő figura mérete éppen kockányi, képsíkja valamelyik közeli kocka-oldal, látványa pedig az ezen felfogott távolabbi kocka-sarkok együtteséből tevődik össze.
Ha a padlóháló középső, függőlegesnek látszó hosszanti fúgáját „csuklópántnak” használva, a végtelenbe futó szomszédos mező-párt megbillentjük, horizontális helyzetből látványosan vertikálisba kerülünk.
A két szomszédos, lebillentett négyzetsor szelete rögzüljön épp derékszögben – íme, eljutottunk a felhőkarcolót képviselő kockatorony tövéből feltáruló látvány esetéhez! Horizontális padlóháló égbeszökő kockatoronnyá alakul.
Példánkban szemsíkunk helyét most valahol a kép alsó szélén is innen érezzük. Ahol a cikk-cakk kiegyenesedik… ott lesz az új horizont! [3]
Átlókkal mindkét határoló síkon tetszés szerint szaporíthatjuk az oldalmezők rész-osztásait. Felülről lefelé haladtunkban az előző iránypont (a torony csúcsa) lassan kicsúszik látókörünkből.
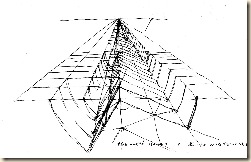
Gyakorlatban úgy járunk el, hogy a befoglaló formán belül vázlatunk közeli függőleges élére rendre fölmérjük a segédvetületről átvihető magasság-rövidüléseket. Az első (alsó) kocka a vázolás kezdetén még eredeti magassággal és függőleges élekkel szerepel. A későbbi pontosítást szemmértékünk is igényli.
Ez számszerűleg is igazolható: egész S-ből tizenegy-tizenketted S lesz az oldalnézeten. Az n-edik emelet 1 / n-1 (azaz 0) magasságú. A kiterített segédvetületből visszaszámolt képtávolság miatt előre felmérhetjük a harmadik iránypont helyét (kb. 3 ¼ S ill. 1 ¼ KT). E szerint az n-edik szinten az alul még testes kocka ponttá zsugorodik! Ez csak akkor valósul meg, ha a szélső függőlegesek szintről-szintre egyre inkább összehajlanak. A köztes födémek négyzetlapjait átlók segítségével ellenőrizhetjük.
Ellivuori, vonalzós perspektíva, 1974 (Suvitie-Uusitalo építésziroda, Tampere)
Az első, befoglaló nagykocka szabadkézzel készült, az összes többi szerkesztés vonalzó segítségével, az átlós módszert ismételgetve. A kihúzás szabadkezes, a tónusok ragasztott fóliával.
GYAKORLATI TANÁCSOK
Három iránypontos perspektíva szerkesztése előtt érdemes előbb messzebbről, két iránypontos tömegvázlatot készíteni. Amikor terpesztett függőlegesekkel módosított, három iránypontos szerkezeti rácsunkat (mint „süveget”) megpróbáljuk ráilleszteni két iránypontos vázlatunkra, az össz-magasság jelentős csökkenését tapasztaljuk.
A befoglaló kockaháló szerkesztése során hasznos kiinduló adatokhoz jutunk papírcsík-módszer szerinti segédvetületeinkről. Ezek közül kiemelten fontos lehet:
• az alsó szint fedlapjának alálátása,
• a felső kocka alálátása, illetve
• a rövidülő emeletmagasságok átvétele.
A ”süveg” karcsúsodása a szélső függőlegesek dőlésétől függ. Az alsó ill. felső emelet össz-szélessége szintén átvihető segédvetületünkről. Az ívesen kirajzolódó kontúr-szakaszok külső érintővel (vagy belső húrral) kiegyenesíthetők. Bár a befoglaló kockarács elindításához hatásosan alkalmazhatjuk segédvetületeink adatsorát – mégse nélkülözhetjük egészséges szemmértékünket, mellyel végül a szerkesztett perspektíva hihetőségét ellenőriznünk kell!
ÖSSZEFOGLALÁS
Az iránypontok száma a szemlélő képsíkja és a téma homloklapja közti viszonytól függ. A kockasorral magyarázható horizontális és vertikális helyzet között analógia van. Kilencven fokkal elforgatott padlóháló felhőkarcoló négyzetrácsos homlokzatává alakul. Harmadik irányponttal akkor lesz dolgunk, amikor kockatornyunkhoz közelebb megyünk. Horizonttól távolodva, az emelet-magasságot egyre fokozottabb mértékű rövidülésben látjuk. Nézőpontunk megválasztásával előre beállíthatjuk az oldallapok és az alálátás arányát. Ha adott méretű ábrát szeretnénk, nem ajánlatos előre kitűzni az iránypontokat.
Vázlatunkban a közeli függőleges skálán rendre felmérjük a segédvetületről leolvasható magasság-rövidüléseket.
Hivatkozások:
[1] „Első kocka – szélső kocka (A Papírcsík-módszer)”
[2] „Fókuszban a térsarok –Hogyan alakítható térszerkesztés tárgy-rajzolássá?”
[3] „Kockarács – a látványterv szerkezeti rácsa”
[4] „Tér mint nagykocka-belső – a Műegyetem Aulája”
[5] „Tükröződő Toronytrió – a szerkezeti rács szélső lapjai”









Nincsenek megjegyzések:
Megjegyzés küldése