Szerkesztési gyakorlat a Harmadik Iránypont témájához
Kulcsszavak: felezősík, nézési irányba forgatott alaprajz, oldallap-arány, padlóhorizont, rögzített iránypont, segédvetület, tapasztalati képtávolság-határ, tárgyképsík, zenit.
FELADAT: Keressük meg a lehető legnagyobb kocka-méretet és a harmadik iránypont helyét (a zeniten) a két oldalt a padlóhorizonton előre rögzített iránypontok függvényében!
Nézőpontunk simuljon padlóvonalba; a közeli kocka-él (S) legyen a lapszélesség harmada táján! A két iránypont t-közti távolság most rajzlapunk hosszabbik oldala.
Figyelmünket kezdetben a legalsó szintre fókuszáljuk, mintha csak egyetlen kockáról lenne szó. Nézőpontunkat helyezzük el egyelőre oda, ahonnan nézve az alsó szint függőlegesei még éppen nem torzulnak.
A tapasztalati képtávolsági határ (II. és III. Ip között) hozzávetőlegesen a tárgyméret két- és-félszerese (KT kb. = 2 ½ S). Ennél közelebbről az egységnyi kocka-él (az átfogó) egyre inkább eltér annak nézőpontunkból rövidülésben látott vetületétől (a befogótól). A felezősíkon felvett segédvetület egymáshoz illesztett, szabályos derékszögű háromszögekkel magyarázza ezt a jelenséget.
A továbbiakban szintről szintre haladva, kockánként magasítjuk tornyunkat.
Rögzített oldalsó iránypontok. Mekkora lehet a még éppen hihető, lehető legnagyobb kocka? Keressük meg az erre építhető kockatorony harmadik iránypontját a zeniten!
Kiinduló adatok: Ip bal, Ip jobb (fekvő A/3-mas lap átellenes peremén) , padló-horizont (H).
Köztes eredmények: képtávolság (KT), közeli kocka-él (S max).
Végül: harmadik iránypont (III. Ip) a kocka-él (S) ill. a képtávolság (KT) függvényében.
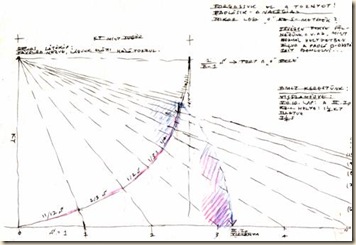
| Kocka-szerkesztés rögzített iránypontokkal (felülnézet). A képet átszelő vízszintes vonal a tárgyképsík vonalát jelzi. |
Az első szakaszban feltételezett kiskocka közeli sarkával a tárgyképsíkra illeszkedik az alaprajzon. Elforgatott helyzetét az adott iránypontok által kitűzött derékszög határozza meg. Visszaszámolt oldalmérete a képtávolság két-ötöde lesz
S = 2/5 KT
Első felülnézeti befoglaló formánk a kisnégyzet átlójával, mint átmérővel megrajzolt kör lesz. Papírcsíkról leolvasható (illetve beállítható) az oldallap-metszékek tervezett aránya (itt: x bal / X jobb = 2 / 3). Ezen túlmenőleg a hátsó, negyedik él helye is átvihető tervünkre. Visszamérve az oldallap-metszékek összegét az eredeti kocka-élhez (x bal + X jobb / S): „hat-ötöd aránylik az egyhez” méretű téglalap adódik.
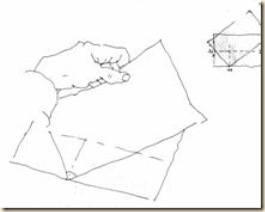
Az adott iránypontokra mutató derékszög kitűzése közönséges írólap sarkának segítségével valósítható meg. Az első feltételezést utólag pontosítjuk. Ezért látszik két, egybevágó, hasonló négyzet a nézési irányba forgatott alaprajzon. A belső négyzet volt az első, feltételezett; a külső négyzet az új, módosított változat.
A második papírcsík szolgáltatja a megoldást: a képtávolság két-ötöde adja a legnagyobb kocka-élet.
A kockaméret módosítása az egybevágó háromszögek elvén történő, arányos nagyítás. Az oldallap-metszékek aránya (itt: kettő a háromhoz) nem változik.
A harmadik iránypont tengelyét a befoglaló forma középvonalában tételezzük fel.
| |
Kiindulásul adottnak vettük a két iránypont közti távolságot. (Példánkban egy A/3-mas fekvő lap két szélén tűztük ki a bal ill. jobb oldali enyészpontot.) A képtávolság 2/5-e lesz a kitűzött iránypontokhoz tartozó, legnagyobb kocka-él (S x 2 ½ = KT).
Az emeleteket jelképező kockákat egyenként vizsgáljuk. Képsíkunk folyamatosan merőlegesen tartandó a célba vett kocka súlypontjára irányított vezérsugárhoz képest!
A papírcsík-módszer szerint (a felezősíknak nevezett) metszeten soronként rögzítjük a szintmagasságok rövidülését (S1 > S2 > S3 > … > Sn). A rövidülés adatsorát a torony talpához illesztett, gömbsüveg-alakú, körívnek látszó képsíkunkon összesítjük.
Felfelé haladtunkban, a körív-metszékek rohamosan rövidülnek
| Első szint: 11 /12 S Második szint: 2 / 3 S Harmadik szint: 1 / 2 S Negyedik szint: 1 / 3 S Ötödik szint: 1 / 4 S… | ||
| |
| |
Hasznos adatokhoz jutunk az alsó szinthez tartozó kocka felvázolásához is. Az alálátás sávja segédvetületünkről olvasható le (Y = ¼ S).
A korábban bemutatott analógia szerint döntsük most padlósíkba a tornyot! Mikor lesz nulla az S-metszék? A torony tövéből ugyanolyan látvány tárul fölénk, mint a távolba tekintve, elénk - padló-négyzetrács esetében (l. MB: Harmadik iránypont papírcsíkkal).
Természetes látómezőnket (nyakforgatás nélkül) kb. 60 fokos látókúp határolja be. Távolba nézvén, talpunknál a padlóháló eltorzul. Az enyészpontot kutatván, emeljük fel kissé tekintetünket!
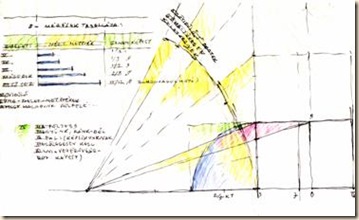
Gömbsüveg-alakú képsíkunk (oldalnézetben: negyed körív) sugara KT. A természetes látókúpban egyszerre látszó emelet-sorokat (ill. padlóháló-szeleteket) mutatja a fenti ábra.
A táblázatot folytatva: az n-edik szintre tekintve, 1 / n-1 a rövidülés mértéke. S tart a nulla felé. Ezt csak akkor látjuk, ha tekintetünket megemeljük - ekkor a lábunk előtti sorok kiesnek látómezőnkből. Állításunk a toronyfalra is igaz: tövéből csúcsára felnézve lábazatát nem láthatjuk.
60 fokos látókúpunkhoz tartozó, rövidülő emeletmagasságok összegét kerestük. A rész-magasságok köríven sorakoznak. Ennek kiterített hosszát visszamérjük az eredeti emeletmagasságot tartalmazó S-skálára. Innen leolvasható a keresett viszony. A harmadik iránypontot (a lehető legnagyobb kocka-él függvényében, rögzített oldalsó iránypontok esetében): nagyjából tizenhárom-negyed kocka-élnyi távolságra találjuk meg a horizont felett.
III. Ip = kb. 3 ¼ S
Vagy másképpen, összevetve az előző ábrával: a harmadik iránypont helye kb. ötnegyed képtávolság:
III. Ip = 1 ¼ KT
Gyakorlatban úgy járunk el, hogy a befoglaló formán belül vázlatunk közeli függőleges élére rendre fölmérjük a segédvetületről átvihető magasság-rövidüléseket.
Az első (alsó) kocka a vázolás kezdetén még eredeti magassággal és függőleges élekkel szerepel. A későbbi pontosítást szemmértékünk is igényli.
Ez számszerűleg is igazolható: egész S-ből tizenegy-tizenketted S lesz az oldalnézeten. Az n-edik emelet 1 / n-1 (azaz 0) magasságú. Kiterített segédvetületből visszaszámolt képtávolság segítségével előre felmérhetjük a harmadik iránypont helyét (III. Ip = kb. 3 ¼ S ).
A köztes födémek négyzetlapjait átlók segítségével ellenőrizhetjük.
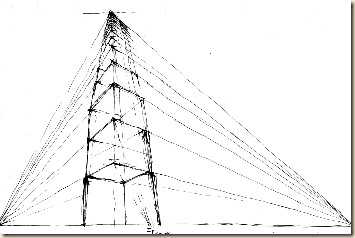
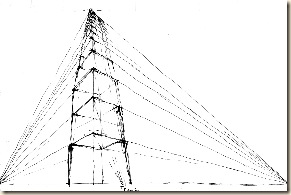 Az n-edik szinten az alul még testes kocka ponttá zsugorodik. Ez csak akkor valósulhat meg, ha a szélső függőlegesek szintről-szintre haladtunkban egyre inkább összehajlanak. |
Kapcsolódó témák:
MB: Harmadik iránypont – papírcsík-módszerrel
MB: Analógia első és harmadik iránypont között
MB: Látványtervek


Nincsenek megjegyzések:
Megjegyzés küldése