Körgyűrűk

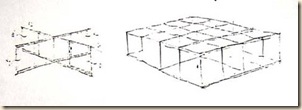
Hengergyűrű szerkesztése befoglaló kockaráccsal

4 x 4 x 1 kiskockából összeállított befoglaló rács

	A befoglaló kockarács tengelykeresztjében sorakozó álló síkú négyzetlapokat - a könnyebb tájékozódás kedvéért - égtáj-létráknak neveztem el.

Kulcs-szavak: befoglaló kockarács, egyszerű geometriai forma (EGF), égtáj-létra, fejvonal, képsík-mozaik, negyed-átló, nyolcadpontos körszerkesztés, palást-alkotó, szerkezeti váz, talpvonal, vetület.

Semmilyen spekulatív szerkesztés nem pótolhatja építészeti szabadkézi rajzban az önálló megfigyelést, amely a látvány saját nézőpontunkhoz tartozó perspektív torzulásait rögzíti arányhelyesen rajzlapunkon.

Gondosan figyeljük meg az ívek (esetleges) összemetsződéseit, az ívek által bezárt (konkáv vagy konvex) lencse-alakzatokat, a (külső, belső, alsó, felső) ívek találkozási pontjait!

Típushibának számít a rálátás eltúlzása, ami általában abból adódik, hogy egy-egy majdnem-igaz részlethez makacsul ragaszkodunk, miközben kis hibáink halmozódva - elviselhetetlenül - összeadódnak.

1 – Szerkezeti rács

Értelmezzük mindenek előtt a jól látható négyzetlapok közti virtuális távolságokat vetületekben is! A kezdetben célszerű pl. égtájak szerint tájékozódni. Így megnevezhetjük a tengelykereszt ágait: észak-déli illetve kelet-nyugati tengely.

A felülnézeten egyértelműen felismerhető a körgyűrű kiskockákból összeállított befoglaló rácsa. A testcsoport bordázatát függőleges síkú négyzetlapok alkotják.

Az átlók révén gondosan ellenőrizzük a 4 x 4-es négyzethálót!

Fekvő hengergyűrű kockarácsos vetületei. A tengelykereszt távlati képen látszik.

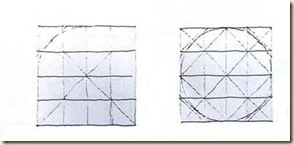
2 - Körszerkesztés

Először felülnézben gyakoroljuk a nyolcadpontos körszerkesztést! A kör négyzetbe írható.

A teljes kört 4 negyedből illesztjük össze. A negyed-négyzetekhez egy-egy negyedkörív tartozik. Minden negyedkörívet három érintőhöz szorítunk. A két szélső érintő a befoglaló negyed-négyzet szomszédos oldalpárja.

A középső (nyolcadponthoz tartozó) érintő a negyedátlóval párhuzamos egyenes, amely csak egy kicsivel van beljebb, mint maga a negyedátló. A befoglaló kereten mért különbség: 1/10 sugár, vagy 1/5 félsugár.

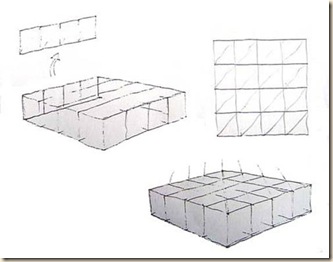
3 - „Égtáj-létrák” elemzése

Egyenként, majd egymáshoz viszonyítva is figyeljük meg az „égtáj-létrákat”! Gondosan ábrázoljuk a nézőpontunkból látható átfedéseket is! Ne feledjük, hogy a teljes befoglaló forma részei a következők: egyik szárny + másik szárny + negatív forma foltjai.

4 – Az „égtáj-létrák” viszonyítása

Az „égtáj-létrákat” (mint képsík-mozaikokat) a főirányok közé szorítjuk. A mozaik szélső határait a legfelső és legalsó pontra illesztett fej- ill. talpvonalak képezik.

5 – Összemetsződések, átfedések, képsík-mozaikok

Ábránkon az égtáj-keretek összemetsződését elemezzük. Főirányokat a szélső pontokra illesztjük. Kiegészítő negatív formákat megvizsgáljuk. Össz-szélesség és össz-magasság viszonyát is eldöntjük. A képsík-mozaikokat egyszerű geometriai formákra bontjuk. Keret-összemetsződéseket is gondosan megfigyeljük...

Példánkban itt pl. az északi keret bal széle harmadával metszi a nyugati keret tetejét ill. az északi keret aljának ¾-e metszi a nyugati keret jobb felét, stb. Azért neveztük el égtájak szerint a tengelykereszt látható lapjait, hogy szövegben is megjeleníthessük nézőpontunkhoz tartozó viszonyaikat!

Az esetleges átfedéseket és köztes foltokat arányméréssel, egyszerű geometriai formákra való bontással elemezhetjük.

6 - Az „égtáj-létrák” kiegészítése

A látványban eddig állósíkú négyzetek és közök rendszeréről volt szó. Most az „égtáj-létrákat” kiegészítjük teljes befoglaló kockarácsra, amelynek kiterjedése: 4 x 4 x 1 egység.

7 - Ellenőrzések

A hátsó négyzet-sor után a felső négyzet-háló kontrollját végezzük el. Mivel az átlók a valóságban párhuzamosak, perspektívában összetartónak látszanak.

8 – Ellipszisek

A teljes körgyűrű szerkezeti hálója tizenhat kiskockából áll. Az alsó ellipszisnél elegendő néhány minimális vonal-darab megkeresése, hiszen a szélső alkotók már ismertek.

Figyeljünk a D-betükre! Az ellipszis legnagyobb kiterjedése nem a felező-alkotónál lesz, hanem - a rálátás miatt - kijjebb (vagy feljebb, lejjebb, aszerint hogy merre mutat a ferde).

Ne mulasszuk el a szerkesztett érintőkhöz simítani az ívet! Hasznos megkeresni a képzeletbeli kábeldobot pallókkal, vastag deszkákkal burkoló palást-alkotókat is. Látványosan elő-tónusozható a palást alkotó-irányú felületosztással, amely a rövidülés miatt sűrűbb vonalkázást eredményez a beforduló szakaszokon, mint a szemből látható íves felületeken.

A kör távlatban ellipszisnek látszik. A kész ellipszis ellenőrzésképpen kis- és nagytengelyén áttükrözendő. Ezek a szimmetria-tengelyek nem feltétlenül azonosak a szerkesztés során használt befoglaló kockarács osztásaival!

9 – Megfigyelések

A szerkesztéssel egyidejű megfigyelések talán egyik legfontosabb állomása a „befoglaló forma” arányának megállapítása, munkánk elején. Gyakran az ívek „egymásba harapnak” (a köztes folt itt vonalkázva látszik), viszonyuk mindenképpen pontosan megfigyelendő. Végül érdemes a befoglaló kontúr keretére az ívek összemetsződéseit kivetíteni.

ÖSSZEFOGLALÁS

A teljes körgyűrű szerkezeti hálója tizenhat kiskockából áll. A szerkesztéssel egyidejű megfigyelések fontos állomása a befoglaló forma arányának megállapítása és az ívek közötti viszony rögzítése. A testcsoport bordázatát valós és látszólagos négyzetlapok alkotják, melyeket a könnyebb tájékozódás kedvéért „égtáj-létráknak” neveztünk el. Ezek egymáshoz viszonyított megfigyelésében rejlik a hengergyűrű szerkezetének kulcsa.

lásd még: http://mehesb.rajzi.bme.hu/perspektiva_kgy.htm